Franzettis Mathematik: Weg zur Maturprüfung
Lasciate ogni speranza, voi ch’entrate!
Ein Buch in 6 Teilen und 30 Kapiteln
Dies ist ein Mathematikbuch, das den Stoff für eine eidgenössische Mathematik-Matura gemäss Richtlinie des Staatssekretariat für Bildung, Forschung und Innovation umfasst. Es geht vom sogenannten normalen Niveau aus und kennzeichnet den Stoff für das erweiterte Niveau.
Es ist im Stil der „Selbststudium“-Bücher verfasst und auf Effizienz angelegt, d.h. der oder die Studierende soll nicht selber die Mathematik neu „erfinden“. Die Didaktik ist äußerst einfach: Theorie erklären, Übungen erläutern, Aufgaben stellen (und Lösungen mitgeben), analog der künstliche Intelligenz von modellieren, trainieren, testen. Das Buch enthält Lösungen zu alten offiziellen Prüfungsaufgaben. Es ist vom Ende her gedacht: was muss man wissen, um die Matura bestehen zu können. Deshalb unterscheidet es sich von den Lehrwerken für die Gymnasien und Mittelschulen in der Gewichtung der Themen.
Das Buch ist keine Aufgabensammlung. Es wird impliziert, dass man alle Aufgaben löst.
Das Buch eignet sich auch als Vorbereitung für das Studium als Repetitorium oder als Vorbereitung für universitäre Aufnahmeprüfungen, z.B. ETHZ und link oder Uni Zürich. Bei der EPFL gibt es einen Selbsttest (französisch).
Hier vorliegend ist ein erster Entwurf. Mit Schreibfehlern ist zu rechnen. Sie haben die Möglichkeit, das Werk besser zu machen, indem sie Kommentare abgeben.

Ein paar Zeilen als Kostprobe
![]()
![]()
Gesucht Lösung für ![]() . Wir schreiben das Reziproke hin, tauschen Zähler und Nenner auf beiden Brüchen
. Wir schreiben das Reziproke hin, tauschen Zähler und Nenner auf beiden Brüchen ![]() und formen um
und formen um
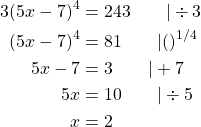
![]()
Hier ein Beispiel, wo wir einen Nicht-Quotienten in einen solchen umformen und dann den Satz anwenden. Wir betrachten ![]() und erweitern mit dem Doppelbruch
und erweitern mit dem Doppelbruch ![]() , ersetzen dann
, ersetzen dann ![]() und
und ![]() mit
mit ![]() . Alles zusammen:
. Alles zusammen:
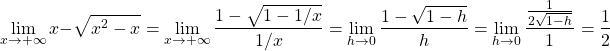
![]()
Gesucht ist die Anzahl Personen, die mindestens eine Katze oder einen Hund besitzen. Nimmt man die Anzahl Personen, die einen Hund halten und addiert die Anzahl Personen, die eine Katze besitzen, dann subtrahiert man die Anzahl Personen, die beides haben.
Wir erinnern uns an die Mächtigkeit von Mengen. Die zwei Mengen Hundebesitzer ![]() und Katzenhalter
und Katzenhalter ![]() sind nicht teilerfremd, haben also eine Schnittmenge
sind nicht teilerfremd, haben also eine Schnittmenge ![]() . Die Mächtigkeit der Tierbesitzer
. Die Mächtigkeit der Tierbesitzer ![]() ist deshalb
ist deshalb ![]() .
.
![]()
Die Varianz bestimmt sich mit denselben Argumenten, wobei noch ein bisschen mehr umgeformt werden muss. Wir verwenden Gleichung~??. Der zweite Term ist einfach
![]()
Der erste ist
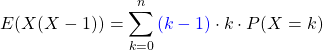
Die rechte Seite unterscheidet sich von der obigen Herleitung nur durch den blauen Term ![]() . Somit können wir ihn bis zur letzten Form einfach stehen lassen und bekommen
. Somit können wir ihn bis zur letzten Form einfach stehen lassen und bekommen
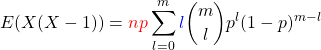
Die Summe ist der Erwartungswert ![]() . Also ist
. Also ist ![]() . Die zwei Teile zusammen ergeben
. Die zwei Teile zusammen ergeben
![]()
